Utilizing the CGA companion module
Introduction
The CGA companion module comes along with and is dependent upon the GALua module. It provides a number of Lua classes, each representative of a geometric primitive of the conformal geometric algebra (CGA) for 3-dimensional space. These geometries are listed in the following table, each accompanied with a loose description.
| Geometry | Description |
| Point | The basic element making up all geometries. |
| Sphere | A set of all points equidistance to a given point. |
| Plane | A set of coplanar points. |
| Line | A set of colinear points. |
| Point-Pair | A set of colinear points equidistant to a given point. |
| Circle | A set of coplanar points equidistant to a given point. |
| Flat-Point | Another point representation of CGA. |
The flat-point has some interesting properties in CGA, one of which is that it is the only geometry of CGA that, when expressed in direct form, cannot be written as the outer product of (round) points. In any case case, this page is not an attempt to teach CGA. For that, I refer the reader to the following list of sources.
- What may have been the original white paper on CGA.
- This book covers CGA in great detail, although I feel it lacks a great deal of rigour. Be sure to consult the errata page.
- A short tutorial on CGA.
An instance of one of the classes of the CGAUtil module is an object representative of a CGA geometry. Being a Lua table, it's entries give the defining characteristics of that geometry. As we know from CGA, however, it is the blades of the Minkownski geometric algebra that are either dually or directly representative of a given piece of geometry. (On the other hand, a given blade simultaneously represents two different geometries: one dually, the other directly. Which we care about is simply a matter of interpretation -- a choice we are free to make.) Where the use of the CGAUtil module comes into play, therefore, is in its ability to convert between such blades and objects (class instances). The conversion from object to blade is known as composition, while the conversion from blade to object is known as decomposition.
To free this tutorial from the great many mathematical details chosen by the CGAUtil module, such details are given at length in the following document, which has been prepared specifically for the CGAUtil module and its documentation.
A great deal of thought and effort has gone into making sure that this math is correct. Any update to the math performed in the CGAUtil module will also be reflected in a change to this document.
All of this said, we're now ready to show how one may go about using the CGAUtil module. We will do so by simply giving a number of examples that illustrate the usage of various features of the module.
Example 1: Fitting a circle to 3 points
We start by simply created 3 points that determine a circle. To determine a circle, they must be non-colinear.
local point1 = cga.NewPoint{ center = cga.evec( -1, 0, 0 ) }:ComposeBlade()
local point2 = cga.NewPoint{ center = cga.evec( 1, 0, 0 ) }:ComposeBlade()
local point3 = cga.NewPoint{ center = cga.evec( 0, 1, 0 ) }:ComposeBlade()
This code illustrates a number of features. First, notice the cga.evec(...) function.
This is a convenience function provided by CGAUtil that allows you to easily formulate euclidean
vectors. It is simply implemented as follows.
function CGAUtil.evec( x, y, z ) return x*e1 + y*e2 + z*e3 end
Secondly, notice the cga.NewPoint(...) function. This function creates and
returns an object representative of a conformal point. Such a function is provided
for all the conformal geometries. The entire list is given in the following table.
| Creation function |
cga.NewPoint(...) |
cga.NewSphere(...) |
cga.NewCircle(...) |
cga.NewPlane(...) |
cga.NewPointPair(...) |
cga.NewLine(...) |
cga.NewFlatPoint(...) |
Tangent points are the degenerate rounds of CGA, and not given their own object. Free blades are not yet supported.
Unlike a consideration we would have concerning a given blade, for any object returned by one of these creation routines, we never care about how that object represents its geometry. For example, an object does not dually or directly represent a CGA geometry. This brings up what may be a confusing point in the semantics of CGA. Geometrically speaking, there is no difference, for example, between a dual sphere and a direct sphere. A sphere is just a sphere. Those terms arrise, however, in an attempt to be more specific about how a given blade represents a certain geometry, but despite the difference in names, it has no bearing on the actual physical geometry to which we are referring.
To be more precise, given any CGA geometry, there exist two blades representative of that geometry: one does so dually, the other directly, and it's not hard to show that these are simply duals of one another. Given any blade, we can choose a dual or direct interpretation of it; and often it is to our advantage to pick between the two the geometry most applicable to the problem we are trying to solve. (You'll see an example of this in the next example.)
Returning to the example at hand, notice that we handed a table to the
cga.NewPoint(...) function. This table is expected to
contain zero or more of the following entries, not all of which are
applicable to conformal points, but may be applicable to other CGA geometries.
We give the full list here for completeness.
| Table Entry Key | Table Entry Value Description | Default Value |
"weight" | A non-zero scalar value. | One |
"center" | A euclidean location vector. | Zero |
"normal" | A unit-length euclidean direction vector. | e1 |
"radius" | A non-negative scalar value. | One |
"imaginary" | A boolean value. | False |
If any one of these table entries is missing, a default will be used. The default values are also listed in the above table.
Thirdly and lastly, notice the ":ComposeBlade() method call. Supported by
all geometry objects of CGAUtil, this function formulates a blade, (as a function of the defining characteristics
of its geometry being represented by the object), that is dually representative of that geometry.
To get the direct representation of the geometry, simply take the dual of the returned result.
Having created our 3 points, we can easily find the circle fitting these points as follows.
local dirCircle = point1 ^ point2 ^ point3 local dualCircle = dirCircle * cga.I local circleObj = cga.NewCircle( dualCircle )
Here we see that instead of passing a table to the creation function, we have passed in a blade dually representative of the computed circle. Doing this, the constructor of the object will attempt to decompose the given blade. Nil is returned if the decomposition fails. All composition functions create a dual geometry as output and all decomposition functions expect a dual geometry as input.
You'll also notice the cga.I constant. This is defined as the unit pseudo-scalar
of our Minkownski geometric algebra. CGAUtil also defines cga.i as the unit pseudo-scalar
of the largest Euclidean geometric sub-algebra of our Minkowski geometric algebra. To be precise about
the sign of these pseudo-scalars, they are defined internally as follows.
no_ni = no ^ ni i = e1 ^ e2 ^ e3 I = i ^ no_ni
Having now created circleObj, we are free to inspect its table entries
to learn about the circle fitting the 3 points.
for key, value in pairs( circleObj ) do print( key .. ": " .. tostring( value ) ) end
Running the entire example, you should get the following, listed in perhaps some other order, of course.
weight: 2 radius: 1 normal: -e3 imaginary: false center: 0 type: circle
If given any object instance, and you are not sure what type of object it may be, you may always
check the type entry of the object table to find out what type of object it is.
Example 2: The point-sphere silhouette problem
Given a sphere and a point some distance from the sphere, imagine viewing the sphere from this distant point. Imagine a circle that outlines the sphere from this perspective. Now, if this circle shared every point with the sphere, what circle would it be? This is the problem we want to solve, and we'll do it with CGAUtil.
A visualization of the problem is given below.
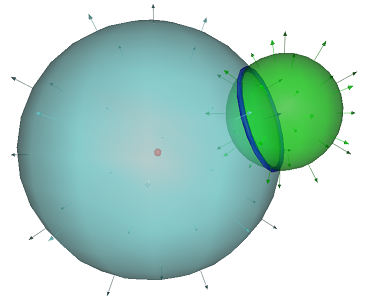
Here, the red point is a flat point, and the sphere in question is the green sphere. By taking two blades, each dually representative of the red point and green sphere, respectively, we consider taking their intersection, which is found by simply taking their outer product. The result is a blade dually representative of the empty point-set geometry, (the geometry of nothing.) However, it can be shown that if we re-interpret this blade in terms of what it directly represents, we get the cyan colored sphere above which has the property of intersecting the green sphere in exactly the circle, (shown above in blue), that is the answer to our problem. Let's go ahead and carry out these calculations using CGAUtil.
local greenSphereBlade = cga.NewSphere{ center = ..., radius = ..., }:ComposeBlade()
local redPointBlade = cga.NewFlatPoint{ center = ... }:ComposeBlade()
local cyanSphereBlade = ( redPointBlade ^ greenSphereBlade ) * cga.I
local blueCircleBlade = greenSphereBlade ^ cyanSphereBlade
local circleObj = cga.NewCircle( blueCircleBlade )
print( "circle center: " .. tostring( circleObj.center ) )
print( "circle radius: " .. tostring( circleObj.radius ) )
Ellipses were placed where actual data should be substituted.
At each step in the process of finding the answer, this code calculates a blade dually representative of the named geometry.
We could have calculated the answer without any need of cyanSphereBlade or cga.I as follows.
local greenSphereBlade = cga.NewSphere{ center = ..., radius = ..., }:ComposeBlade()
local redPointBlade = cga.NewFlatPoint{ center = ... }:ComposeBlade()
local blueCircleBlade = greenSphereBlade .. ( redPointBlade ^ greenSphereBlade )
Example 3: The inversion of a circle in a sphere
Suppose now that we wish to invert a circle in a sphere. For some it may be obvious as to what we generally get when performing such an operation. It is most often a circle, but sometimes a line. In any case, if we're not sure what the result of any operation is, we can use CGAUtil's general decomposition method to find out.
local yellowCircleBlade = cga.NewCircle{ center = ..., radius = ..., normal = ..., }:ComposeBlade()
local orangeSphereBlade = cga.NewSphere{ center = ..., radius = ..., }:ComposeBlade()
local redUnknownGeometryBlade = orangeSphereBlade * yellowCircleBlade * orangeSphereBlade:inverse()
local geoObjList = cga.Decompose( redUnknownGeometryBlade )
if #geoObjList > 1 then
for _, geoObj in geoObjList do
local redKnownGeometryBlade = geoObj:ComposeBlade()
print( geoObj.type .. ": " .. tostring( redKnownGeometryBlade ) )
end
else
error( "Decomposition failure!" )
end
Note that the taking of an inverse here is not really necessary since the inverse of the sphere blade (a vector) is just a scalar multiple of that vector.
A picture of the situation we have here is given as follows.
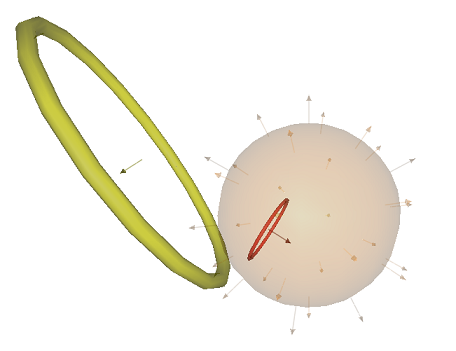
As you can see, the general decomposition method (cga.Decompose(...)) returns a list
geometries. There is nothing complicated about this method. It simply tries all decomposition methods
for each type of CGA geometry, and returns the list of those that successfully decomposed, the idea
being that a given blade is a given geometry if and only if it successfully decomposes as such.
This puts the responsibility of correct geometric identification on the individual decomposition methods
for eacy type of CGA geometry.
Conclusion
This concludes the CGAUtil tutorial. At the time of this writing, CGAUtil is still a work in progress, but as it stands now, allows you to use much of what CGA has to offer. For example, although we didn't cover any of the more complicated conformal transformations, they are, of course, available to you by virtual of your own knowledge of how such transformations are formulated and applied in CGA. We need not make any specific reference to such things in CGAUtil, because, as we know in CGA, the geometries of CGA are also the transformations of CGA, which is quite interesting. Support for composing and decomposing specific types of transformations, however, is on the list of things to do for CGAUtil.
