

This was a fun puzzle, because it gave me some trouble. It's a generalization of the skewb. I don't have the Skewb documented, because the solution was revealed to me, and I'm only trying to take notes on solutions I've found myself.
For a long time I didn't touch this puzzle, because it turned so poorly that it wasn't fun to play with at all. But I would turn it occasionaly and over time, I think it loosened up enough that I was willing to start analyzing it.
For my solve, we label the cube as follows.
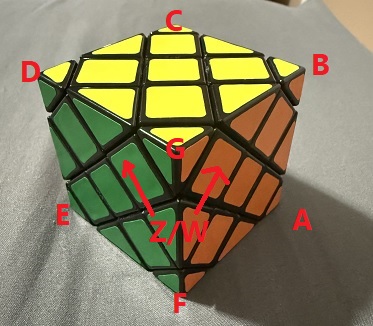
Here, 7 of the 8 corners of the cube are labeled. The remaining corner on the other side of the cube will be denoted H. The Z and W axes represent middle slices and when rotating clock-wise, go in the direction indicated by the arrows.
There are 4 classifications of pieces on this puzzle: corners, edges, centers and off-centers. There are 6 center pieces (1 per face) and 24 off-center pieces (4 per face.)
Solve the corners and centers as you would a regular Skewb.
Solve the off-center pieces. I used Q,H,Q',H' where Q=Y,Z',Y' and Y=A,Z,D. It took a lot of effort to figure this one out, and maybe there's a better sequence, but in any case, the net effect of this sequence is shown in the following pictures. The sequence was applied to a solved cube, so it's easy to see where pieces went and which were preserved.


The first of these pictures was taken from the perspective at which the sequence was executed. The second rotates the cube around 180 degrees. Note that the sequence did not change the face that is in contact with the table.
As you can see, the sequence does a pair of tri-cycles: one that tri-cycles off-center faces, and one that tri-cycles edges. Use this sequence, in conjunction with setups, to get all off-centers pieces into position.
Lastly, solve the edges. I used T,D,T',D' with T=Z,W,Z',W'. This tri-cycles 3 edges in the top of the cube, and its inverse is easy to remember. I don't think that the orientation of the edges is ever a problem. You just need to get them into position.
It strikes me as interesting that this final sequence is simpler than the one presented in Step 2. Usually the opposite is true. That is, sequences that are more targeted (permute less of the cube and preserve more of it) are more complex than sequences that permute more and preserve less.