Gem 8

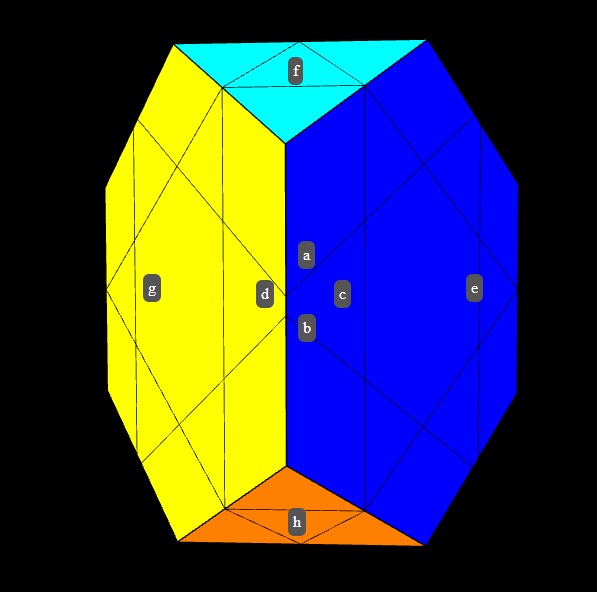
This is another puzzle I don't actually own, so I figured out how to solve it using my twisty-puzzle software. Our labeling will be as follows.

There are 5 classes of faces: hexagonal centers, triangular centers, bow-tie edges, corners, and triangular faces adjacent to the hexagonal centers. I'll call these latter faces just regular triangular faces for short.

Step 1

Solve the bow-tie edges. Solving them in a single face is easy and intuitive. An obvious tri-cycle to solve the remainder is easy. If they're all positioned correctly, except that two are oriented wrong, then use (c',d,c,d'),(a,d',a',d').

Step 2

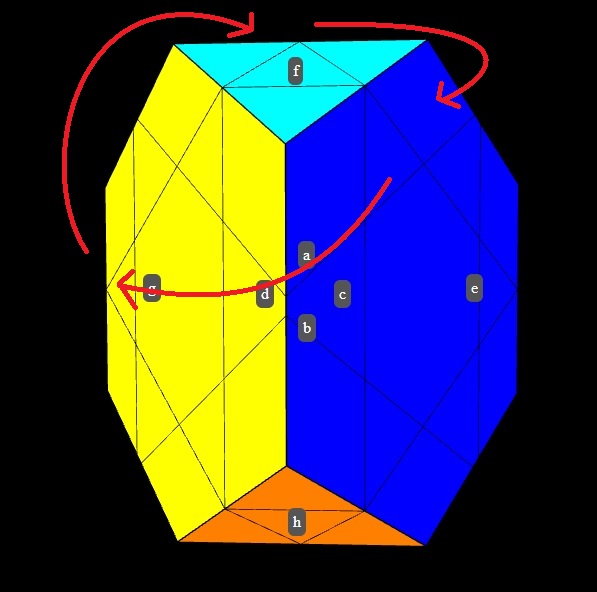
Solve the regular triangular faces. Use X=(c,d',c',d'),f,(c,d',c',d')' (with setups, of course), which tri-cycles as follows.

Step 3

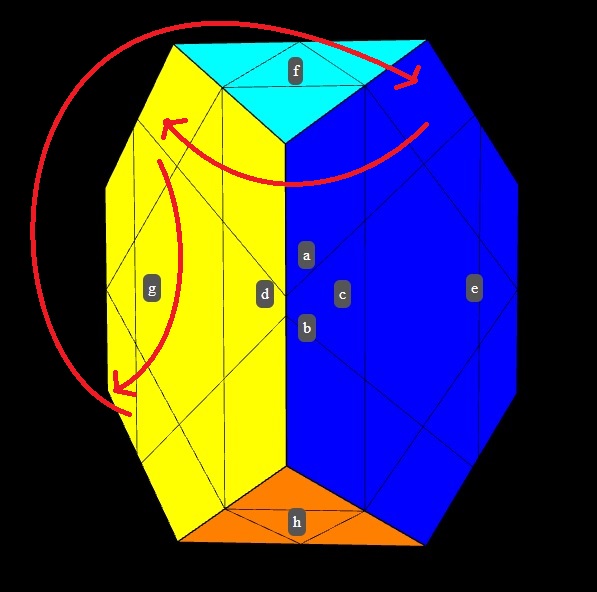
Now solve the corner pieces. Interestingly, a permutor of the corners that preserves everything else can be found using X from the previous step. It is f',d',X,d, and gives the following tri-cycle.

Step 4

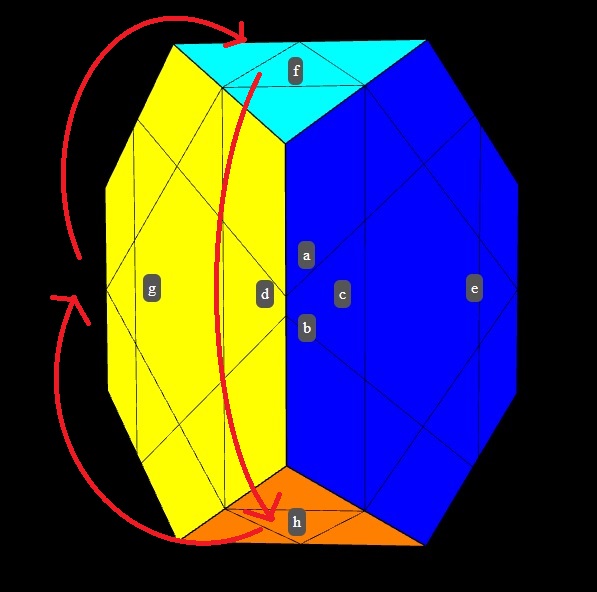
Lastly, solve the triangular faces. They can be permuted with 4(a,b,c,d), which gives the following tri-cycle.

Admittedly, this sequences wasn't found by any sort of reasoning. I just happened upon it. The software greatly helps in discovering such sequences. And often, that's how you come up with any solution. You just try obvious commutators, or commutators of commutators, or maybe not so obvious commutators, and then just see what they do to an already solved puzzle. If the outcomes seems desirable, then you combine it with setup moves (make conjugates with them.)