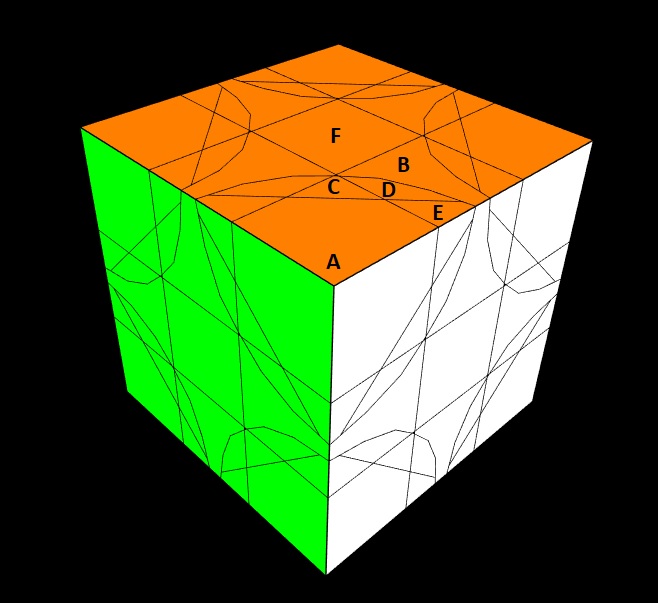
The following figure will be used in my solution outline.

Here I have labeled the class of faces, and also what may be thought of as the class of "cubies" or parts that make up the puzzle.
Simply rotate all corners (class A parts) so as
to restore cube-shape as far as possible. Of course, there will
still be plenty of class D and E parts
poking out, and parts of class C sunken in.
Here we restore cube-shape. I begin with one strategy which works quite well for some time until a different strategy must be employed to finish things up.
The first strategy is to build sandwiches of class E
parts with those of class D. Specifically,
a class E part is sandwiched between two class D parts.
Once the sandwich is built, a corner rotation parks it in one of 2 slots
available in a part of class B. This corner rotation, however,
must not unpark any other sandwich you've built and parked, so be sure to
move things around in prepartion for the parking. Furthermore, this rotation
will undo step 1 in at least one corner (class A part.) To remedy
this, build your next sandwich using parts near this class A part,
or find 3 unsolved sandwiches, locate them about the class A part,
then twist that part to restore step 1.
This strategy will, however, only get you so far. The second strategy is
to first forget about the class D parts, and only focus on
getting the class C and E parts into their proper
orbits. There is a trivial tri-cycle you can use to do this. Once all such
parts are in their proper orbits, use 3[R,RUB,Ri,RUFi] to flatten
the parts of class D.
As just a point of interest, note that 6[R,RUB,Ri,RUFi] can be used
to permute the class E and C parts without unflattening
the parts of class D, although this sequence is not necessary for
the solution being given here.
Next we align colors between the parts of class E and D.
This is a lot of work, but easy to accomplish. After getting things ready, simply
use RUFi,RUB,R,RUBi,2Ri,RUF or something like 3RUF,3LUB,2U,3RUF,3LUB.
Each of these does a pair of color swaps between parts of class D.
(Or you could think of it as swapping parts of class E.)
Note that we are ignoring the parts of class C in this step.
We now align colors for parts of class C with those of class A,
and do so, of course, without undoing step 3. This can be accomplished with all the moves
of step 3; all that differs is the setup. Make sure that you're only doing pairs of swaps between
parts of class D of the same color.
Note that what may be a more efficient way to get this step done is to find your pair of
swaps between parts of class D and E that doesn't undo step 3,
(because you're swapping between same colors), then re-use this swap over and over while
simply slotting whole corners (composites of parts of class A and C)
into and out of the needed locations. This must be done with the 3RUF,3LUB,2U,3RUF,3LUB sequence.
With all sandwiches now solved in terms of both color and shape, it's time to park
them where they belong color-wise. This is trivial until perhaps near the end where
a single tri-cycle cannot finish the step. If you find that a pair of sandwiches need
to swap to complete the step, then execute a sequence such as RUFi,RUB,R,RUBi,2Ri,RUF
or 3RUF,3LUB,2U,3RUF,3LUB in such a way as to not undo step 4. Doing so is simply
a matter of making sure that you're swapping between same colors for parts of class D
and E as well as C and A. Having performed the null-swap, if
you will, the sandwiches should now solve using tri-cycles. Note that if you are careful about
which null-swap you do, it can minimize the number of tri-cycles needed to complete the step.
Lastly, now that we've reduced the puzzle to a 3x3x3, solve it as such. If you find that a single corner is twisted near the end, simply twist that corner into its proper orientation, then tri-cycle the sandwiches into their proper locations.